Origamisan

Okuma Odası → Sangaku ve Origami Probleminin Çözümü 2009-03-11 19:01

Sangaku ve Origami’nin Problemimizi çözen oldu mu bilemiyoruz ama biz cevabını gösterelim. Eğer sorumuzu ilk defa görüyorsanız ilk önce sorumuza bakmanızı tavsiye ediyoruz.

Sorumuz şöyleydi: Kare şeklindeki bir Origami kağıdının bir köşesini karşısındaki kenara gelecek şekilde katladığımızda oluşan üçgenin içerisine çizilecek dairenin yarı çapını ölçmeden nasıl hesaplarız?

A′EF üçgeni dik ve AE=EA′ (1.1)
A′EF üçgeninin içine bir daire çizelim yarı çapı r’ olsun
FC’= A’C’-A’F (1,2)
FB=AB-(AE+EF) ve AE=EA′ olduğundan
FB=AB-(EA′+EF) (1,3)

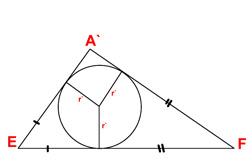
EF= (A’F-r’) + (EA’-r’) dolayısiyle 2r’=A’F + EA’-EF (1,4)

A′EF üçgeni ile BC’F üçgeni benzer oldukları için
r’/A′F=r/BF >> r’ . BF=r . A′F
(1,3) e göre r’.[(AB-(EA′+EF)] =r.A′F r’.AB – r’.(EA′+EF) =r.A′F (1.5)

Aynı şekilde
r’/EF=r/C’F r’.AB – r’.(EA′+EF) =r.A′F r’ . C’F=r . EF
(1,2) e göre r’.(A’C’-A’F) =r.EF r’.A’C’ – r’.AF =r.EF (1.6)

(1.5) den (1.6) yi karşılıklı çıkarırsak

r’.(AB – A’C’-EA′-EF+A’F) =r.(A′F-EF)

A’C’ = AB (Aynı karenin kenarları) olduğundan

r’.(A’F-EA′-EF) =r.(A′F-EF)

2r’=A’F + EA’-EF (1,4) olduğuna göre

1/2(A’F + EA’-EF).(A’F-EA′-EF) =r.(A′F-EF)
1/2((A’F -EF)+ EA’).((A’F-EF)-EA′) =r.(A′F-EF)
1/2((A’F -EF)²-EA’²) =r.(A′F-EF)
1/2(A’F² -2A’F .EF+EF²-EA’²) =r.(A′F-EF)

EF²=A’F²+EA’² (Pisagor bağıntısı)

1/2(A’F² -2A’F .EF+A’F²+EA’²-EA’²) =r.(A′F-EF)
(A’F² -A’F .EF) =r.(A′F-EF)
A’F(A’F-EF)=r.(A′F-EF)
Sonuç olarak A’F=r olarak bulunur

• Youtube
• Video